凯利公式计算器：股票 / 基金仓位怎么控制？算清最优投注比例，降低亏损风险

在2025年的投资市场中，股票和基金波动性加大，仓位控制成为投资者避免爆仓、实现长期增长的关键。凯利公式（Kelly Criterion），一种源于信息论的数学模型，由约翰·凯利于1956年提出，后被投资大师爱德华·索普应用于金融领域。它帮助投资者计算最优投注比例，最大化财富的几何增长率，同时降低破产风险。本文将详细解析凯利公式的原理、计算方法，并通过实际案例展示如何应用于股票和基金投资。无论您是新手还是资深玩家，掌握这一工具都能提升决策科学性，避免盲目加仓导致的损失。

凯利公式的核心原理

凯利公式本质上是一种优化策略，旨在通过计算每次投资的最优比例，实现长期资金的最大化增长。它假设投资机会独立且重复出现，强调“几何平均回报”而非简单算术平均。这意味着，即使短期亏损，长期也能通过合理仓位实现复利增长。

标准凯利公式为：

在赌博中简单易懂：如抛硬币游戏，正面赢1倍，反面输全部，p=0.6，b=1，则f* = (1*0.6 - 0.4)/1 = 0.2，即每次投注20%资金。

但在股票/基金投资中，需调整为更一般形式，以适应部分损失场景：

或针对连续回报的版本：

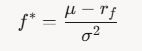
其中，μ\muμ是预期年化回报率，rfr_frf​是无风险利率，σ\sigmaσ是年化波动率。这类似于夏普比率的变体，用于量化投资。

例如，在股票投资中，p可视为策略的胜率，b为平均盈利/平均亏损比率。通过历史数据或回测估计这些参数，计算出最优仓位，避免过度杠杆导致的“赌徒破产”。

凯利公式在股票/基金中的应用

在股票市场，凯利公式常用于仓位管理，尤其在趋势跟踪或价值投资策略中。假设您有100万元资金，投资一只股票，预计胜率p=60%，平均盈利率为20%（b=0.2/0.1=2，如果平均亏损10%），则f* = (2*0.6 - 0.4)/2 = 0.4，即每次投资40万元。

对于基金，如指数基金，波动较低，可用连续模型。2025年，假设沪深300基金预期回报μ=8%，无风险利率r_f=2%，波动率σ=15%，则f* = (0.08 - 0.02)/(0.15)^2 ≈ 2.67。但由于f* >1表示杠杆，实际需调整为半凯利（f*/2=1.335），建议借贷投资，但风险高。

凯利公式的优势在于数学严谨：投注过多（如全仓），短期波动可能清零资金；投注过少，增长缓慢。通过计算器，您可输入参数，模拟不同场景，避免情绪化决策。

如何使用凯利公式计算器

2025年，许多金融App（如雪球、东方财富）和在线工具提供免费凯利计算器。使用步骤简单：

1. 输入参数：胜率p、赔率b（或预期回报、波动率）。
2. 选择模式：赌博式（离散）或投资式（连续）。
3. 调整风险：全凯利激进，半凯利（f*/2）保守，适合新手。
4. 模拟结果：计算器输出最优仓位，并模拟1000次蒙特卡洛路径，显示长期财富曲线。

例如，使用计算器输入：p=55%，b=1.5（平均盈利1.5倍亏损），f* = (1.5*0.55 - 0.45)/1.5 ≈ 0.25。即25%仓位。如果总资金50万元，则单笔投资12.5万元。

高级计算器还整合实时数据：链接Yahoo Finance或Wind数据库，自动估算股票的μ和σ。2025年，随着AI普及，一些工具如ChatGPT插件可语音输入参数，快速输出。

实际案例：股票投资中的凯利应用

假设小王投资科技股，历史回测显示胜率p=65%，平均盈利/亏损比b=2.5。使用凯利公式：f* = (2.5*0.65 - 0.35)/2.5 = 0.51。即51%仓位。

如果全仓（忽略凯利），短期牛市获利丰厚，但熊市（如2022年科技股暴跌）可能亏损80%，资金腰斩。按凯利，分散到多笔，长期增长率可达原策略的1.5倍。

另一个基金案例：小李投资余额宝式货币基金，μ=3%，r_f=2%，σ=1%，f* = (0.03-0.02)/0.0001 = 100，但实际限为1（全仓），显示低风险资产适合重仓。

这些案例源于投资大师如索普的实践：他在 blackjack 和股票中应用凯利，实现了20%年化回报。

优点、风险与优化建议

优点：

• 最大化增长：理论上，实现最高几何回报。
• 风险控制：避免过度投注，降低破产概率。
• 适用广泛：股票、基金、加密货币均可。

风险：

• 参数估计误差：p和b基于历史，可能不准，导致过度仓位。
• 非独立事件：市场相关性高，公式假设独立，可能高估f*。
• 心理压力：全凯利波动大，建议用分数凯利（f*/k，k=2-4）。

优化建议：

1. 回测数据：用Python或Excel模拟至少5年历史。
2. 多元化：结合多资产，降低σ。
3. 定期审视：2025年市场多变，每季度更新参数。
4. 工具辅助：下载凯利Excel模板，或用在线计算器验证。
5. 专业咨询：结合基本面分析，非纯数学决策。

通过凯利公式，您能科学控制仓位，转败为胜。

（免责声明：本文仅为教育和信息目的，不构成投资建议。股票、外汇、债券等交易涉及重大风险，包括但不限于技术风险、市场风险和监管风险。任何投资决策都应基于充分的研究和专业咨询。）